lblbk.github.io

Batch Normalization

这篇是对 bn 使用中个人问题的总结并不是论文翻译

BatchNorm 是 2015 年由Google 提出，这段时间经常遇到 BN 中问题，以前觉得自己理解了，其实还有很多小细节没有搞懂，因此写一篇详解

Normalization

Normalization是一个统计学中的概念，我们可以叫它归一化或者规范化，它并不是一个完全定义好的数学操作(如加减乘除)。它通过将数据进行偏移和尺度缩放调整，在数据预处理时是非常常见的操作，在网络的中间层如今也很频繁的被使用。

对于图像而言，做法是将每个像素减去图像中所有像素的均值，然后再除以所有像素的标准差，将所有像素值缩放到同一个尺度。归一化的主要目标是提供一种不变性，不变性主要针对的是平均像素强度和对比度的波动，拍摄时的光照强度，图像反射率等会使图片不同区域的像素强度和对比度发生变化，而归一化的目的就是通过尺度缩放弱化这种波动，使得较亮的部分变暗一些，较暗的部分变亮一些。对于大量来自不同分布和来源的图片来说是非常重要的预处理步骤，消除了对比度以及像素强度的波动对特征提取的影响，使得卷积神经网络可以提取稳定的图像特征

详解 BN

深度学习中的 Internal Covariate Shift

深度神经网络模型的训练为什么会很困难？其中一个重要的原因是，深度神经网络涉及到很多层的叠加，而每一层的参数更新会导致上层的输入数据分布发生变化，通过层层叠加，高层的输入分布变化会非常剧烈，这就使得高层需要不断去重新适应底层的参数更新。为了训好模型，我们需要非常谨慎地去设定学习率、初始化权重、以及尽可能细致的参数更新策略。

Google 将这一现象总结为 Internal Covariate Shift，简称 ICS. 什么是 ICS 呢？@魏秀参在一个回答中做出了一个很好的解释：

大家都知道在统计机器学习中的一个经典假设是“源空间（source domain）和目标空间（target domain）的数据分布（distribution）是一致的”。如果不一致，那么就出现了新的机器学习问题，如 transfer learning / domain adaptation 等。而 covariate shift 就是分布不一致假设之下的一个分支问题，它是指源空间和目标空间的条件概率是一致的，但是其边缘概率不同，即：对所有
\[x \in \chi, P_s(Y|X=x)=P_t(Y|X=x)\]
但是
\[P_s(X)\neq P_t(X)\]
大家细想便会发现，的确，对于神经网络的各层输出，由于它们经过了层内操作作用，其分布显然与各层对应的输入信号分布不同，而且差异会随着网络深度增大而增大，可是它们所能“指示”的样本标记（label）仍然是不变的，这便符合了covariate shift的定义。由于是对层间信号的分析，也即是“internal”的来由。

ICS 会导致什么问题？

简而言之，每个神经元的输入数据不再是“独立同分布”。

其一，上层参数需要不断适应新的输入数据分布，降低学习速度。

其二，下层输入的变化可能趋向于变大或者变小，导致上层落入饱和区，使得学习过早停止。

其三，每层的更新都会影响到其它层，因此每层的参数更新策略需要尽可能的谨慎。

BN 原理

“对于一个拥有d维的输入x，我们将对它的每一个维度进行标准化处理。” 假设我们输入的x是RGB三通道的彩色图像，那么这里的d就是输入图像的channels即d=3，标准化处理也就是分别对我们的R通道，G通道，B通道进行处理。

在Normalization完成后，Google的研究员仍对数值稳定性不放心，又加入了两个参数gamma和beta，即 $y^k=\gamma^k \hat{x}^k + \beta^k$, $\gamma$ 是再缩放参数，$\beta$ 是再平移参数，为了保证模型的表达能力不因为规范化而下降，除了充分利用底层学习的能力，另一方面的重要意义在于保证获得非线性的表达能力。举个例子，在sigmoid激活函数的中间部分，函数近似于一个线性函数（如下图所示），使用BN后会使归一化后的数据仅使用这一段线性的部分，如果只用这一段，那网络就成了线性网络。

参数的更新，原文也给了公式

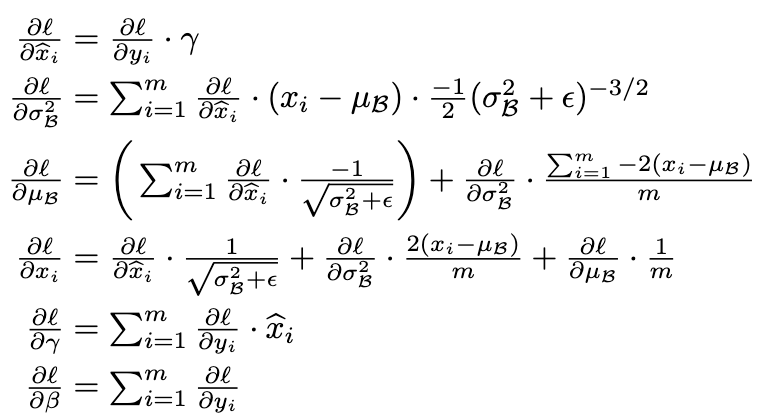
pytorch 的 BN 实现解析

CLASS torch.nn.BatchNorm2d(num_features, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)

momentum – the value used for the running_mean and running_var computation. Can be set to None for cumulative moving average (i.e. simple average). Default: 0.1

This momentum argument is different from one used in optimizer classes and the conventional notion of momentum. Mathematically, the update rule for running statistics here is $\hat{x}_\text{new} = (1 - \text{momentum}) \times \hat{x} + \text{momentum} \times x_t$ , where $\hat{x}$ is the estimated statistic and $x_t$ is the new observed value.

track_running_stats – a boolean value that when set to True, this module tracks the running mean and variance, and when set to False, this module does not track such statistics, and initializes statistics buffers running_mean and running_var as None. When these buffers are None, this module always uses batch statistics. in both training and eval modes. Default: True

BatchNorm 默认打开 track_running_stats，因此每次 forward 时都会依据当前 minibatch 的统计量来更新 running_mean 和 running_var。

Pytorch中的BN层的动量平滑和常见的动量法计算方式是相反的, momentum 默认值为 0.1，控制历史统计量与当前 minibatch 在更新 running_mean、running_var 时的相对影响。

\[running\_mean=running\_mean*(1-momentum)+E(x)*momentum\] \[running\_var=running\_var*(1-momentum)+Var(x)*momentum\]

$E(x)$ $Var(x)$ 分别表示 $x$ 的均值、方差；需要注意这里统计方差时用了无偏估计，与论文保持一致。

在训练过程中model.train()，train过程的BN的统计数值—均值和方差是通过当前batch数据估计的。

并且测试时，model.eval()后，若track_running_stats=True，模型此刻所使用的统计数据是Running status 中的，即通过指数衰减规则，积累到当前的数值。否则依然使用基于当前batch数据的估计值。

BN 冻结

正确的冻结BN的方式是在模型训练时，把BN单独挑出来，重新设置其状态为eval (在model.train()之后覆盖training状态）.

def set_bn_eval(m):
    classname = m.__class__.__name__
    if classname.find('BatchNorm') != -1:
      m.eval()

model.apply(set_bn_eval)

[参考]

详解深度学习中的Normalization，BN/LN/WN - 知乎 (zhihu.com)

深度学习中 Batch Normalization为什么效果好？ - 言有三的回答 - 知乎

PyTorch 源码解读之 BN & SyncBN：BN 与多卡同步 BN 详解 - 知乎 (zhihu.com)

总体、样本、总体方差、样本方差、抽样方差和标准误 - 知乎 (zhihu.com)

Batch Normalization详解以及pytorch实验_霹雳吧啦Wz-CSDN博客