lblbk.github.io
卷积
记录一下常见卷积实现方法,代码是c++版本
朴素卷积
卷积基本原理很简单, 对应每个位置相乘再相加就好,具体代码, 这里不考虑padding或者stride以及其他操作, 根据公式套一下就出来
for (int i = 0; i < o_height; i++) {
for (int j = 0; j < o_width; j++) {
for (int p = 0; p < kernel_h; p++) {
for (int q = 0; q < kernel_w; q++) {
out_data.data[i * o_height + j] +=
in_data.data[(i + p) * width + j + q] *
kernel.data[p * kernel_w + q];
}
}
}
}
im2col gemm Winograd
未整理完成 dcn 双线性卷积 可分离卷积
卷积(convolution)是深度学习中非常有用的计算操作,主要用于提取图像的特征。
一、卷积的基本属性
卷积核(Kernel):卷积操作的感受野,直观理解就是一个滤波矩阵,普遍使用的卷积核大小为3×3、5×5等;
步长(Stride):卷积核遍历特征图时每步移动的像素,如步长为1则每次移动1个像素,步长为2则每次移动2个像素(即跳过1个像素),以此类推;
填充(Padding):处理特征图边界的方式,一般有两种,一种是对边界外完全不填充,只对输入像素执行卷积操作,这样会使输出特征图的尺寸小于输入特征图尺寸;另一种是对边界外进行填充(一般填充为0),再执行卷积操作,这样可使输出特征图的尺寸与输入特征图的尺寸一致;
通道(Channel):卷积层的通道数(层数)。
如下图是一个卷积核(kernel)为3×3、步长(stride)为1、填充(padding)为1的二维卷积:
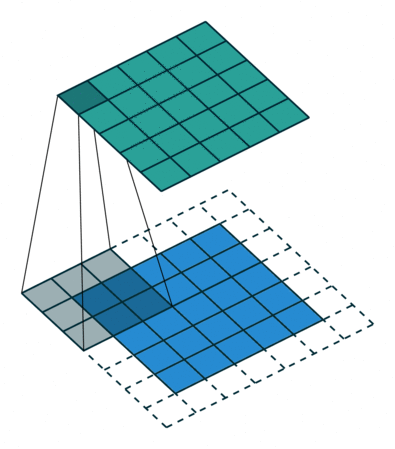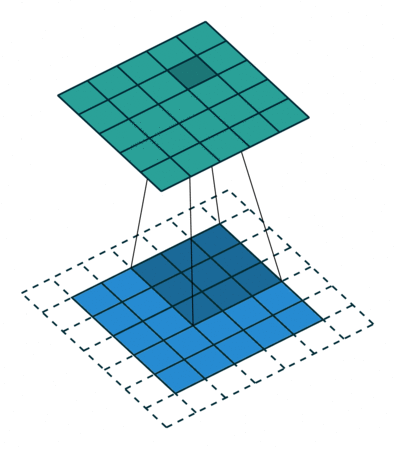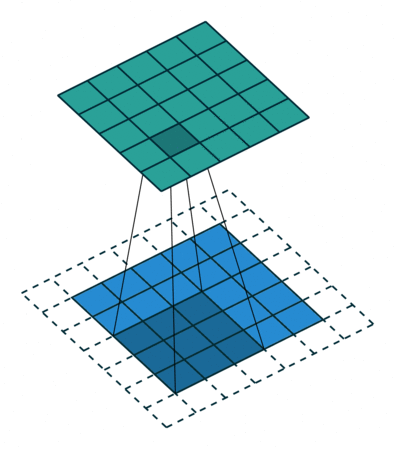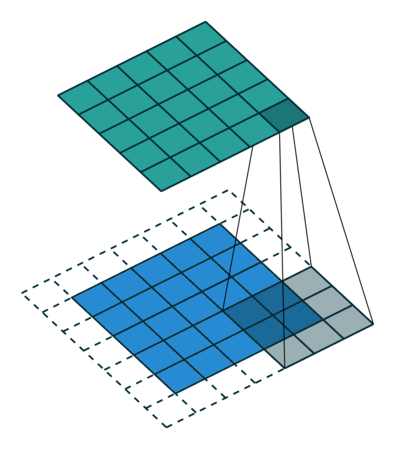
二、卷积的计算过程
卷积公式:
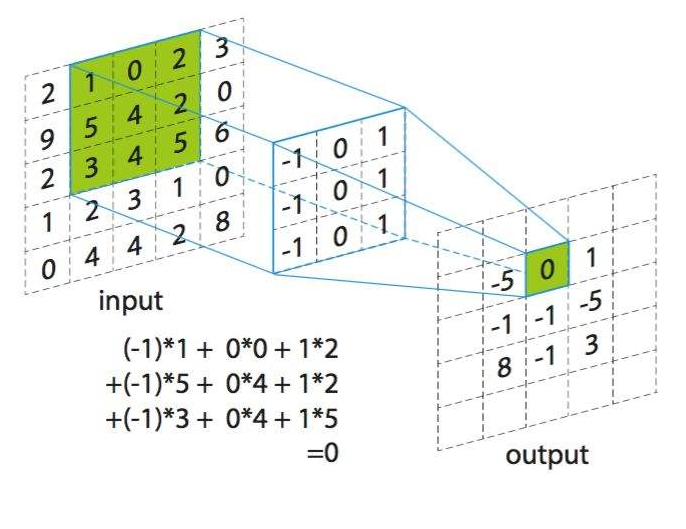
\[w(s, t)*f(x, y)=\sum^{a}_{s=-a}\sum^{b}_{s=-b}w(s, t)*f(x-s, y-t)\]卷积的计算过程非常简单,当卷积核在输入图像上扫描时,将卷积核与输入图像中对应位置的数值逐个相乘,最后汇总求和,就得到该位置的卷积结果。不断移动卷积核,就可算出各个位置的卷积结果。如下图:
三、卷积的各种类型
卷积现在已衍生出了各种类型,包括标准卷积、反卷积、可分离卷积、分组卷积等等,下面逐一进行介绍。
1、标准卷积
(1)二维卷积(单通道卷积版本)(2D Convolution: the single channel version)
只有一个通道的卷积。
如下图是一个卷积核(kernel)为3×3、步长(stride)为1、填充(padding)为0的卷积:
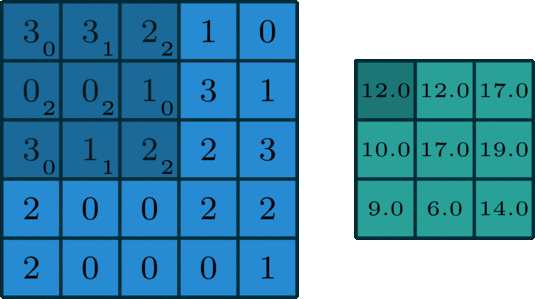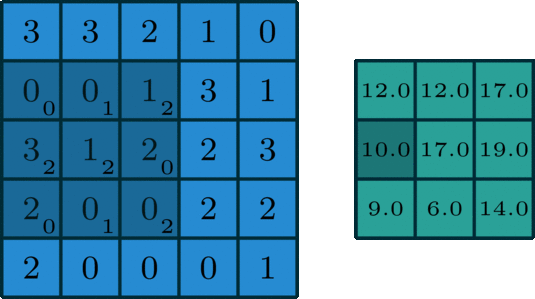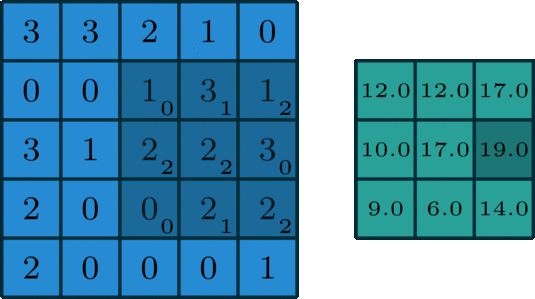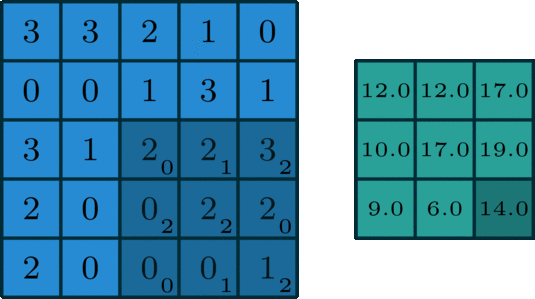
(2)二维卷积(多通道版本)(2D Convolution: the multi-channel version)
拥有多个通道的卷积,例如处理彩色图像时,分别对R, G, B这3个层处理的3通道卷积,如下图:
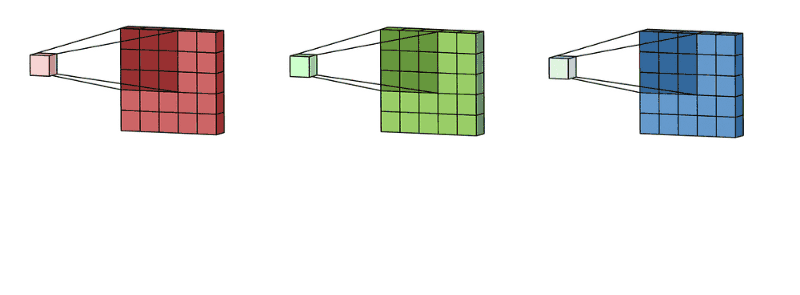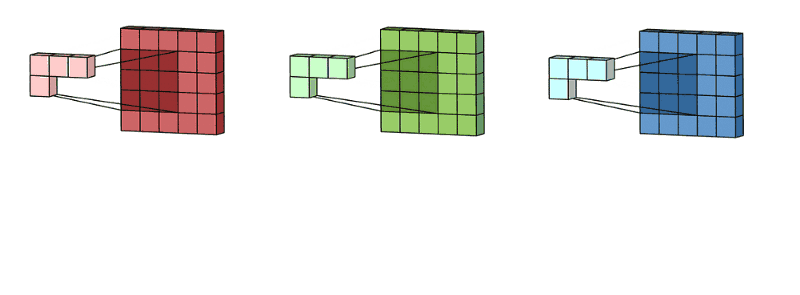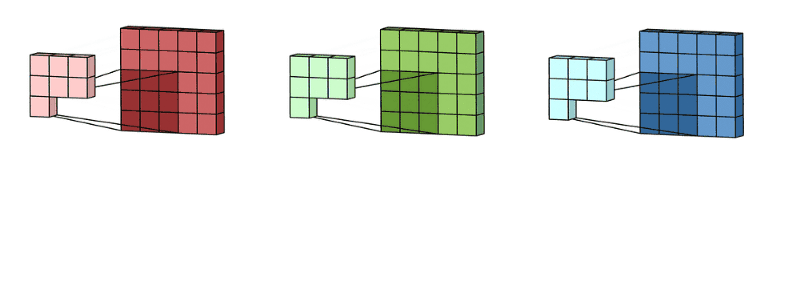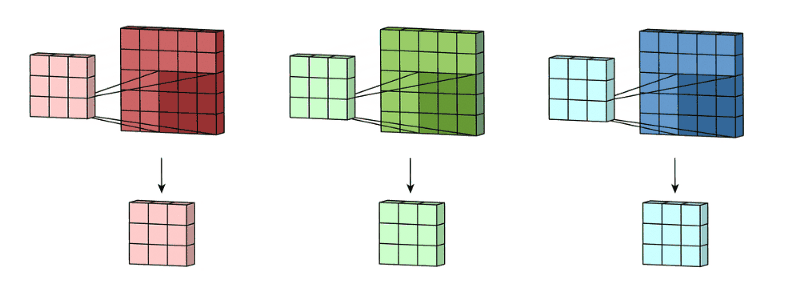
再将三个通道的卷积结果进行合并(一般采用元素相加),得到卷积后的结果,如下图:

(3)三维卷积(3D Convolution)
卷积有三个维度(高度、宽度、通道),沿着输入图像的3个方向进行滑动,最后输出三维的结果,如下图:
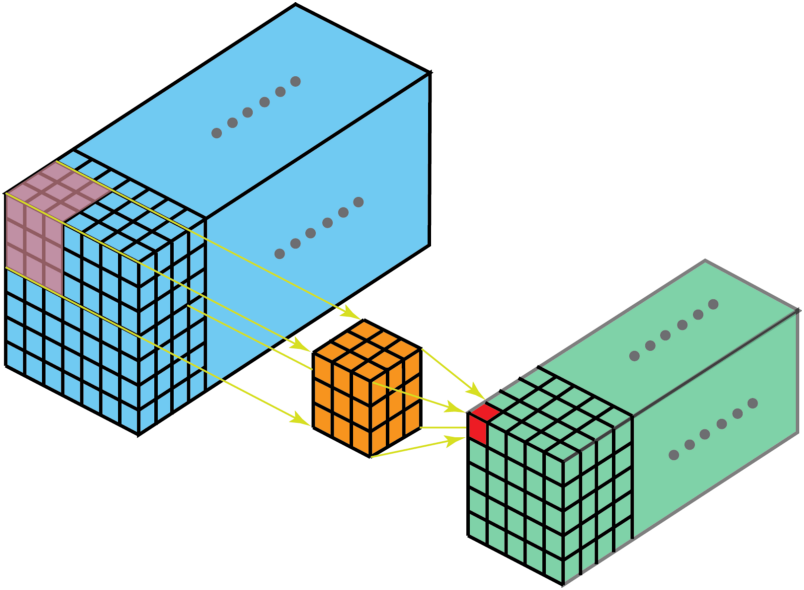
(4)1x1卷积(1 x 1 Convolution)
当卷积核尺寸为1x1时的卷积,也即卷积核变成只有一个数字。如下图:
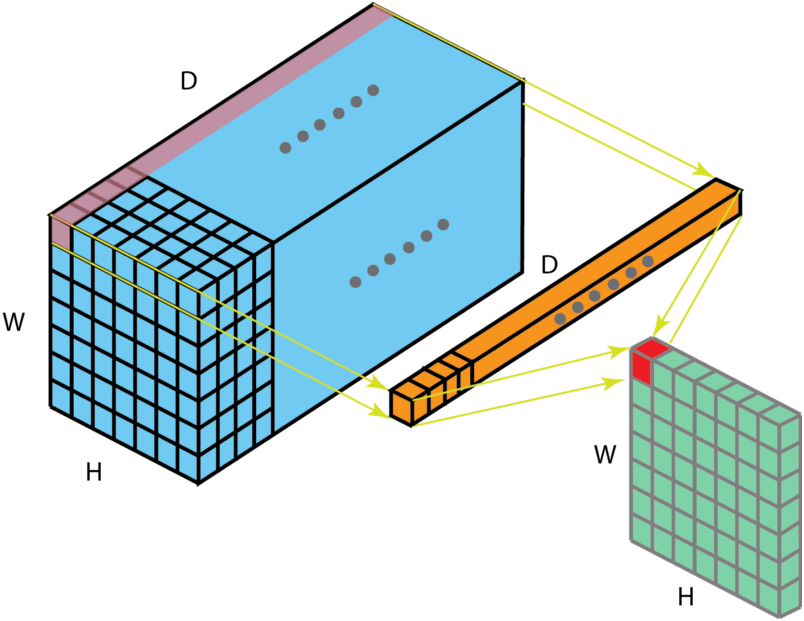
从上图可以看出,1x1卷积的作用在于能有效地减少维度,降低计算的复杂度。1x1卷积在GoogLeNet网络结构中广泛使用。
2、反卷积(转置卷积)(Deconvolution / Transposed Convolution)
卷积是对输入图像提取出特征(可能尺寸会变小),而所谓的“反卷积”便是进行相反的操作。但这里说是“反卷积”并不严谨,因为并不会完全还原到跟输入图像一样,一般是还原后的尺寸与输入图像一致,主要用于向上采样。从数学计算上看,“反卷积”相当于是将卷积核转换为稀疏矩阵后进行转置计算,因此,也被称为“转置卷积”
如下图,在2x2的输入图像上应用步长为1、边界全0填充的3x3卷积核,进行转置卷积(反卷积)计算,向上采样后输出的图像大小为4x4
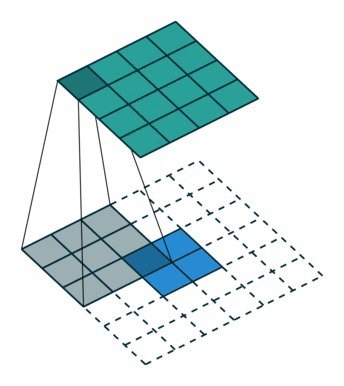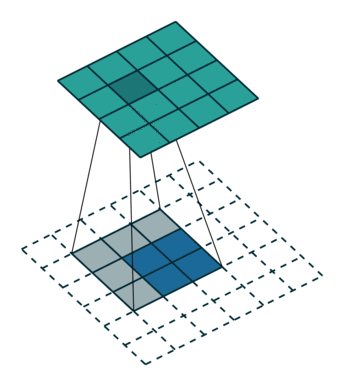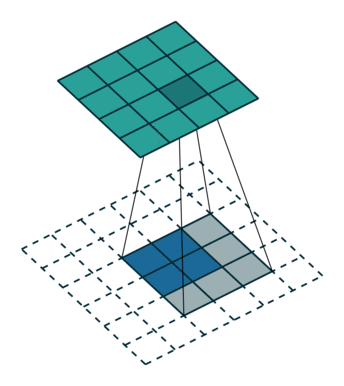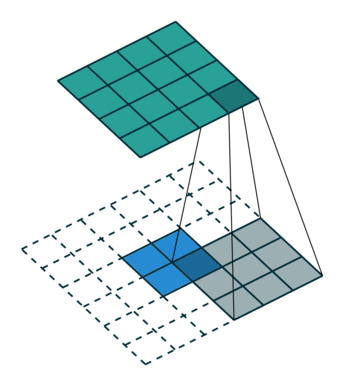
3、空洞卷积(膨胀卷积)(Dilated Convolution / Atrous Convolution)
为扩大感受野,在卷积核里面的元素之间插入空格来“膨胀”内核,形成“空洞卷积”(或称膨胀卷积),并用膨胀率参数L表示要扩大内核的范围,即在内核元素之间插入L-1个空格。当L=1时,则内核元素之间没有插入空格,变为标准卷积。
如下图为膨胀率L=2的空洞卷积:

4、可分离卷积(Separable Convolutions)
(1)空间可分离卷积(Spatially Separable Convolutions)
空间可分离卷积是将卷积核分解为两项独立的核分别进行操作。一个3x3的卷积核分解如下图:
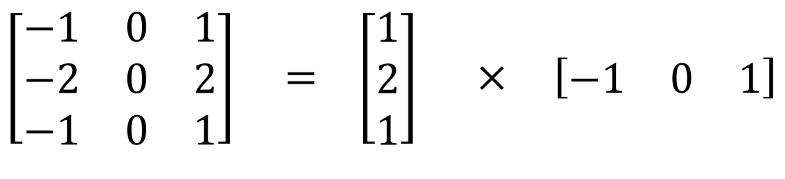
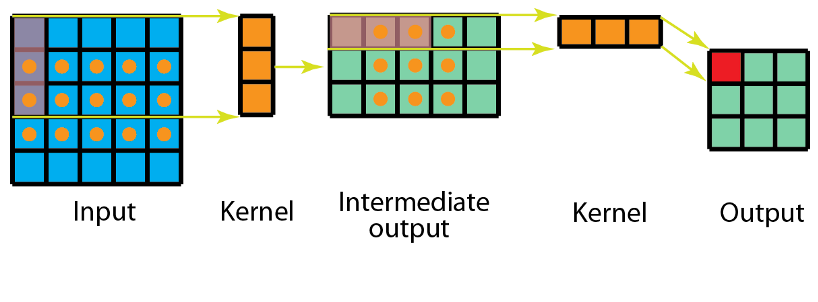
分解后的卷积计算过程如下图,先用3x1的卷积核作横向扫描计算,再用1x3的卷积核作纵向扫描计算,最后得到结果。采用可分离卷积的计算量比标准卷积要少。
(2)深度可分离卷积(Depthwise Separable Convolutions)
深度可分离卷积由两步组成:深度卷积和1x1卷积。
首先,在输入层上应用深度卷积。如下图,使用3个卷积核分别对输入层的3个通道作卷积计算,再堆叠在一起。
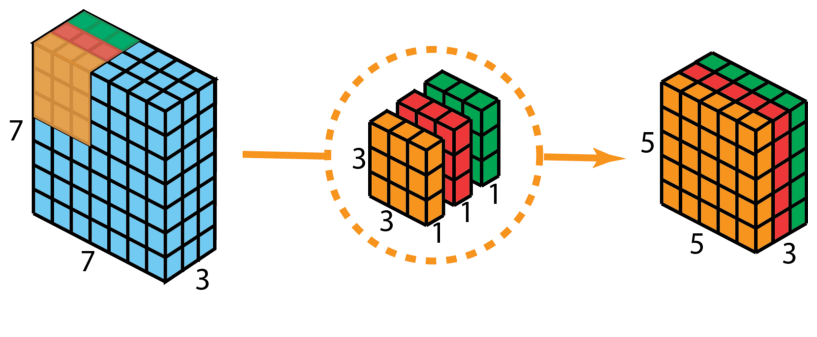
再使用1x1的卷积(3个通道)进行计算,得到只有1个通道的结果
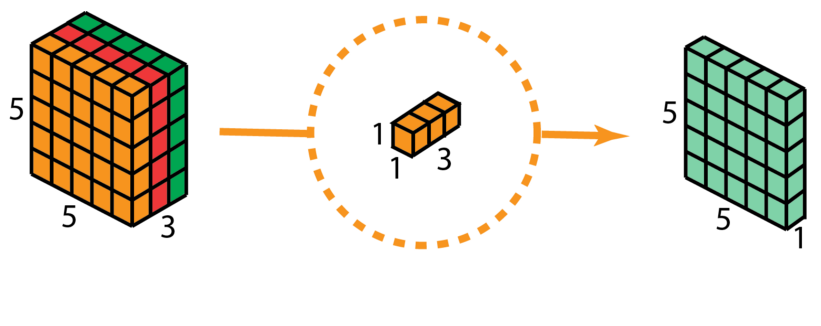
重复多次1x1的卷积操作(如下图为128次),则最后便会得到一个深度的卷积结果。
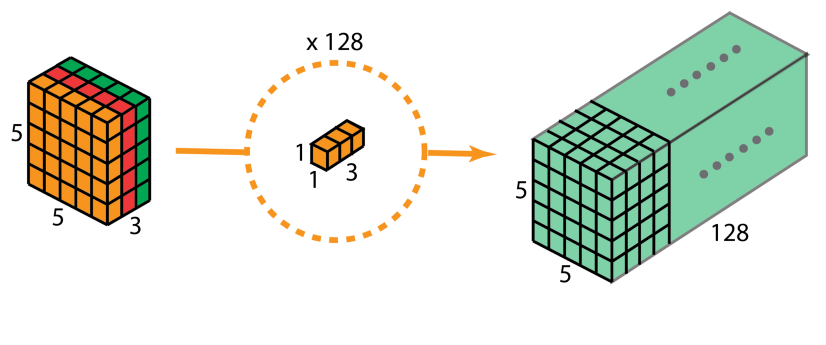
完整的过程如下:
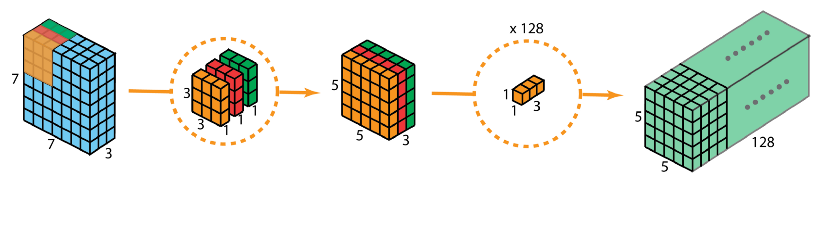
5、扁平卷积(Flattened convolutions)
扁平卷积是将标准卷积核拆分为3个1x1的卷积核,然后再分别对输入层进行卷积计算。这种方式,跟前面的“空间可分离卷积”类似,如下图:
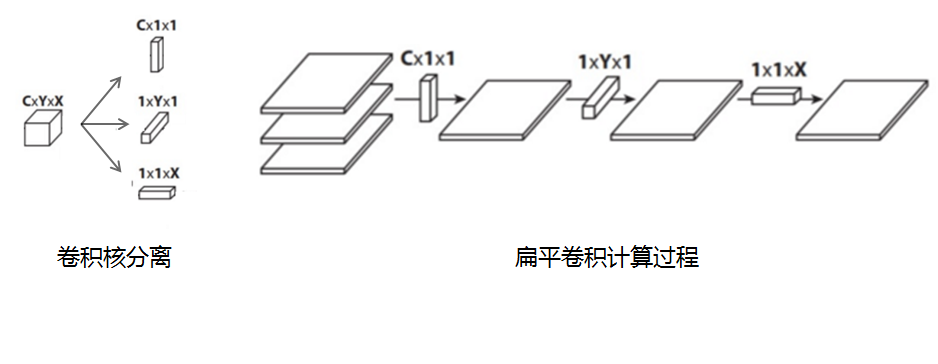
6、分组卷积(Grouped Convolution)
2012年,AlexNet论文中最先提出来的概念,当时主要为了解决GPU显存不足问题,将卷积分组后放到两个GPU并行执行。
在分组卷积中,卷积核被分成不同的组,每组负责对相应的输入层进行卷积计算,最后再进行合并。如下图,卷积核被分成前后两个组,前半部分的卷积组负责处理前半部分的输入层,后半部分的卷积组负责处理后半部分的输入层,最后将结果合并组合。
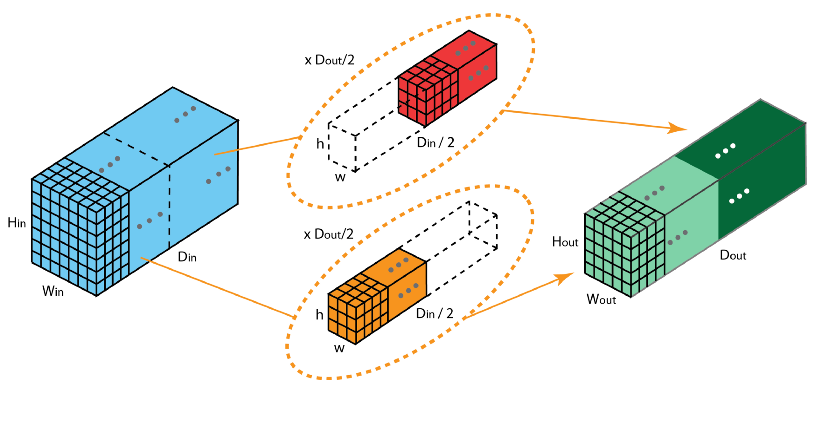
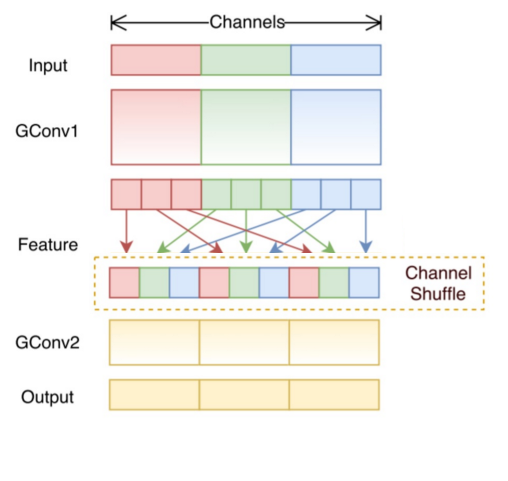
7、混洗分组卷积(Shuffled Grouped Convolution)
在分组卷积中,卷积核被分成多个组后,输入层卷积计算的结果仍按照原先的顺序进行合并组合,这就阻碍了模型在训练期间特征信息在通道组之间流动,同时还削弱了特征表示。而混洗分组卷积,便是将分组卷积后的计算结果混合交叉在一起输出。
如下图,在第一层分组卷积(GConv1)计算后,得到的特征图先进行拆组,再混合交叉,形成新的结果输入到第二层分组卷积(GConv2)中: