lblbk.github.io
数据结构与算法-排序
前言
本来是在写 yolov3 博客,最近发现一直在被面试题虐,而且大部分题目都是考研期间用过的查找和排序,索性总结一篇
分类
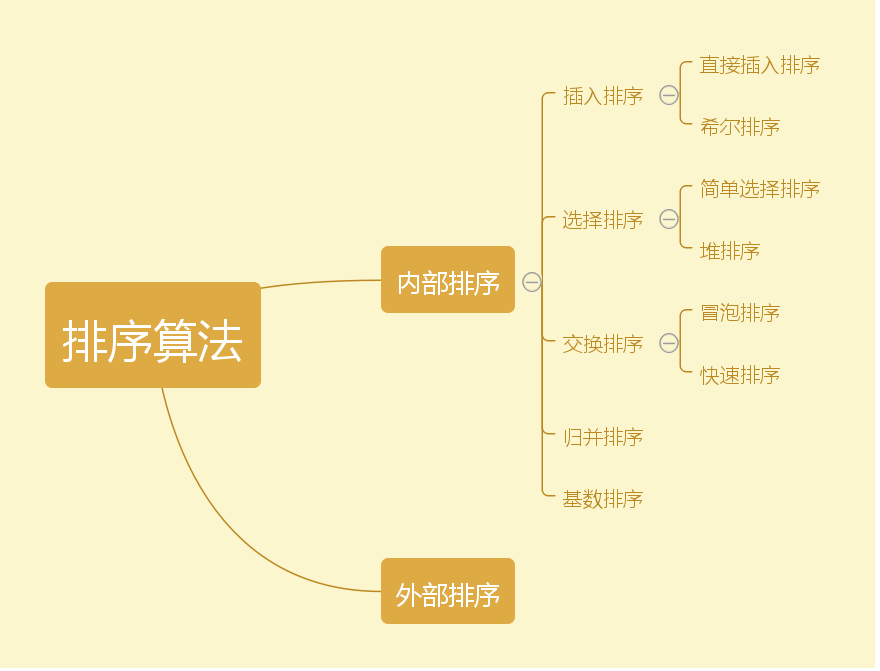
首先排序分为:
内部排序:将需要处理的所有的数据都加载到内部存储器中进行排序
外部排序:当数据量过大,无法全部加载到内存中,需要借助外部存储器进行排序
内部排序又可分为五类,总共细分为八类
性能比较
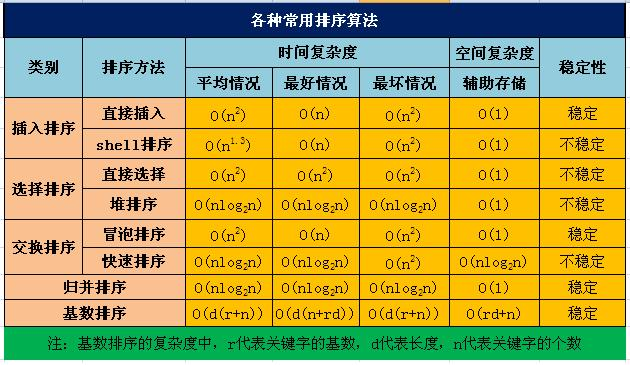
测试代码
void pprint(string sometext, int plt[], const int max_size)
{
printf("%s\n", sometext.c_str());
for(int i=0; i<max_size; i++)
{
printf("%d ", plt[i]);
}
printf("\n");
printf("%s\n", sometext.c_str());
}
int main(int argc, char **argv) {
const int MAX_SIZE = 10;
int in_arr[MAX_SIZE] = {8,1,9,7,2,4,5,6,10,3};
pprint("---Before---", in_arr, MAX_SIZE);
// quicksort(in_arr, MAX_SIZE);
pprint("---After---", in_arr, MAX_SIZE);
return 0;
}
参考资料
这里各种算法排序的动态图,就不放上来了,太占空间
https://leetcode.cn/circle/article/ccqGqW/
插入排序
直接插入排序
思想:把待排序的记录按照值的大小逐个插入到一个有序的序列中
过程
- 这是所有元素后移一个位置
void insertionsort(int arr[], int max_size)
{
for (int i=1; i<max_size; i++)
{
int temp = arr[i];
int k = i - 1;
while(k >= 0 && arr[k] > temp)
k--;
//腾出位置插进去,要插的位置是 k + 1;
for(int j = i ; j > k + 1; j--)
arr[j] = arr[j-1];
//插进去
arr[k+1] = temp;
}
}
- 前后位置交换
void insertionsort2(int arr[], int max_size)
{
for (int i = 1; i < max_size; i++)
{
int temp = arr[i];
int j = i;
while (j >= 1 && temp < arr[j - 1])
{
arr[j] = arr[j - 1];
j--;
}
arr[j] = temp;
}
}
详细参考🔎 https://blog.csdn.net/weixin_62254935/article/details/123449395
希尔排序
原数组的一个元素如果距离它正确的位置很远的话,在插入排序中需要与相邻元素交换很多次才能到达正确的位置,希尔排序就是为了加快速度简单地改进了插入排序,交换不相邻的元素以对数组的局部进行排序。
思想: 先选定一个整数gap,把待排序文件中所有记录分成gap个组,所有距离为gap的记录分在同一组内,并对每一组内的元素进行排序
然后将gap逐渐减小重复上述分组和排序的工作
当到达gap=1时,所有元素在统一组内排好序
void shellSort(int *a, int len)
{
int i, j, k, tmp, gap; // gap 为步长
for (gap = len / 2; gap > 0; gap /= 2) { // 步长初始化为数组长度的一半,每次遍历后步长减半,
for (i = 0; i < gap; ++i) { // 变量 i 为每次分组的第一个元素下标
for (j = i + gap; j < len; j += gap) { //对步长为gap的元素进行直插排序,当gap为1时,就是直插排序
tmp = a[j]; // 备份a[j]的值
k = j - gap; // k初始化为i的前一个元素(与i相差gap长度)
while (k >= 0 && a[k] > tmp) {
a[k + gap] = a[k]; // 将在a[i]前且比tmp的值大的元素向后移动一位
k -= gap;
}
a[k + gap] = tmp;
}
}
}
}
选择排序
直接选择
从未排序元素中寻找到最小(大)元素,然后放到已排序的序列的末尾。以此类推,直到全部待排序的数据元素的个数为零
void selectsort(int arr[], int max_size)
{
for (int i=0; i<max_size-1; i++)
{
int index = i;
// 选择最小的元素
for (int j=i+1; j<max_size; j++)
{
if (arr[j] < arr[index])
index = j;
}
if (index != i)
{
// 交换
int temp = arr[index];
arr[index] = arr[i];
arr[i] = temp;
}
}
}
堆排序
待补充…
void swap(int arr[], int x, int y) {
int key = arr[x];
arr[x] = arr[y];
arr[y] = key;
}
void sift_down(int arr[], int start, int end) {
// 计算父结点和子结点的下标
int parent = start;
int child = parent * 2 + 1;
while (child <= end) { // 子结点下标在范围内才做比较
// 先比较两个子结点大小,选择最大的
if (child + 1 <= end && arr[child] < arr[child + 1]) child++;
// 如果父结点比子结点大,代表调整完毕,直接跳出函数
if (arr[parent] >= arr[child])
return;
else { // 否则交换父子内容,子结点再和孙结点比较
swap(arr[parent], arr[child]);
parent = child;
child = parent * 2 + 1;
}
}
}
void heap_sort(int arr[], int len) {
// 从最后一个节点的父节点开始 sift down 以完成堆化 (heapify)
for (int i = (len - 1 - 1) / 2; i >= 0; i--) sift_down(arr, i, len - 1);
// 先将第一个元素和已经排好的元素前一位做交换,再重新调整(刚调整的元素之前的元素),直到排序完毕
for (int i = len - 1; i > 0; i--) {
swap(arr[0], arr[i]);
sift_down(arr, 0, i - 1);
}
}
交换排序
冒泡排序
它的工作原理是每次检查相邻两个元素,如果前面的元素与后面的元素满足给定的排序条件,就将相邻两个元素交换。当没有相邻的元素需要交换时,排序就完成了
经过 i 次扫描后,数列的末尾 i 项必然是最大的 i 项,因此冒泡排序最多需要扫描 n-1 遍数组就能完成排序
void bubblesort(int arr[], int max_size)
{
bool flag = true;
while(flag)
{
flag = false;
for (int i=0; i<max_size-1; i++)
{
if (arr[i]>arr[i+1])
{
flag = true;
int temp = arr[i];
arr[i] = arr[i+1];
arr[i+1] = temp;
}
}
}
}
快速排序*
分治算法
https://oi-wiki.org/basic/divide-and-conquer/
快排
快速排序分为三个过程:
- 将数列划分为两部分(要求保证相对大小关系);
- 递归到两个子序列中分别进行快速排序;
- 不用合并,因为此时数列已经完全有序
这里有一些优化算法,后续有时间更新
https://oi-wiki.org/basic/quick-sort/
https://blog.csdn.net/m0_63325890/article/details/127195045
https://www.cnblogs.com/MAKISE004/p/16909610.html
void quicksort(int arr[], int l, int r)
{
if (l < r)
{
int i=l, j=r, dummy=arr[l];
while(i<j)
{
while(i<j && arr[j]>=dummy)
j--;
if(i<j)
arr[i++] = arr[j];
while(i<j && arr[i]<dummy)
i++;
if(i<j)
arr[j--] = arr[i];
}
arr[i] = dummy;
quicksort(arr, l, i-1);
quicksort(arr, i+1, r);
}
}