lblbk.github.io
C++ 内存表示
起源
最近一直在研究c++, 在使用指针的时候遇到问题,就通过lldb调试程序,可是得到的结果自己一直看不懂,一度以为c++内存有其他说法, 这里记录一下
问题
起初源于这段代码
float* a = new float[4];
for (int i=0; i<4; i++) {
a[i] = (float)i;
}
当我要去看内存的时候,我一度以为是自己没找对地方
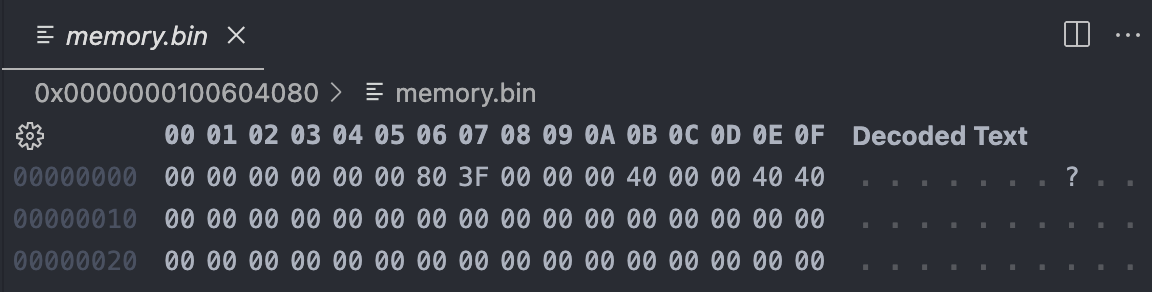
这个我完全没看懂和我存储的值[0, 1, 2, 3]有任何关系,这里我又选择了其他两种方案,直接在vs code输入gdb命令查看,以及通过函数打印,结果一样
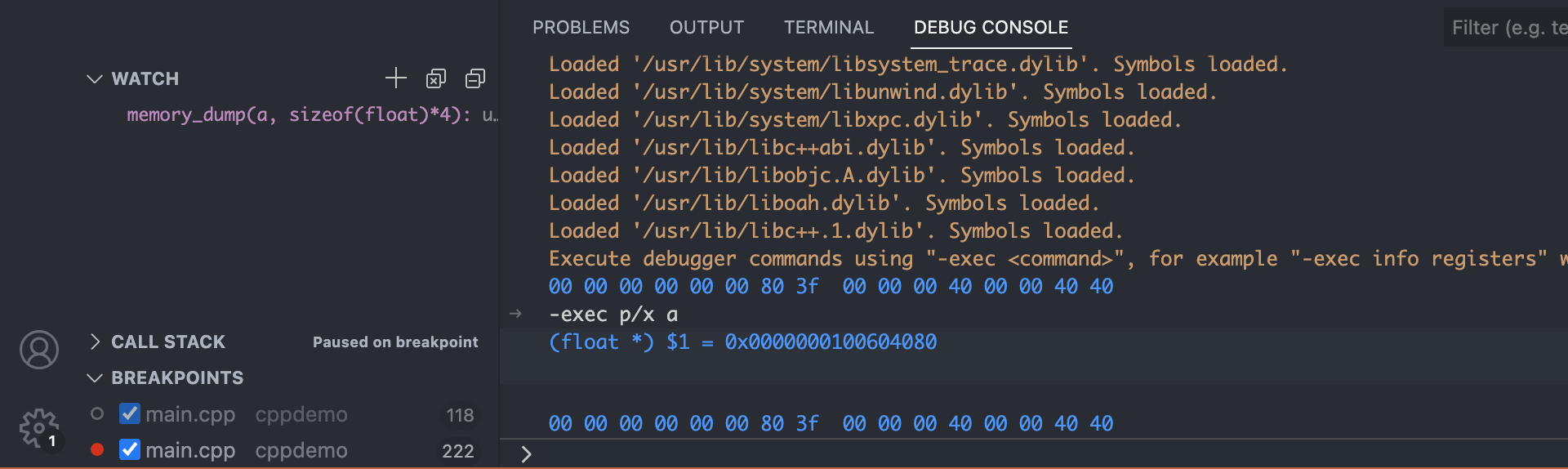
这里大概说一下三种方式
Hex Editor - Visual Studio Marketplace 这个插件可以直接让你看到内存信息
vscode+cmake方式编写的话,debug模式下可以直接调用gdb命令,只需加上
-exec command硬核方式自己写
void memory_dump(void *ptr, int len) { int i; for (i = 0; i < len; i++) { if (i % 8 == 0 && i != 0) printf(" "); if (i % 16 == 0 && i != 0) printf("\n"); printf("%02x ", *((uint8_t *)ptr + i)); } printf("\n"); }上图很形象了,在
watch加上函数和想查看的变量就好了
整型
这时候我就想通过整形数值去测试结果
int* a = new int[4];
for (int i=0; i<4; i++) {
a[i] = i;
}
这里打印的是
00 00 00 00 01 00 00 00 02 00 00 00 03 00 00 00
11 00 00 00 11 00 00 00 11 00 00 00 11 00 00 00
这里看着好像有那么一点靠谱,但是我就是对不上号
00 00 00 00 -> 0
01 00 00 00 -> 64
02 00 00 00 -> ?
03 00 00 00 -> ?
大端 小端
什么是大端和小端
Little-Endian就是低位字节排放在内存的低地址端,高位字节排放在内存的高地址端 Big-Endian就是高位字节排放在内存的低地址端,低位字节排放在内存的高地址端
举个例子,数值 0x12345678,其中 0x12 这一端是高位字节,0x78 这一端是低位字节
大端
低地址 -----------------> 高地址
0x12 | 0x34 | 0x56 | 0x78
小端
低地址 ------------------> 高地址
0x78 | 0x56 | 0x34 | 0x12
大端模式符合我们阅读和书写的方式,都是从左到右的。比如 12345678,我们只需要按照从左到右的顺序进行阅读和书写就是大端模式的存储顺序了
小端模式比较符合我们人类的思维模式,大的放大的那一边,小的放小的那一边。但是在计算机中存储的顺序与我们看到的顺序是相反的
普通数据存储
16bit宽的数0x1234在Little-endian模式(以及Big-endian模式)CPU内存中的存放方式(假设从地址0x4000开始存放)为
| 内存地址 | 小端模式存放内容 | 大端模式存放内容 |
|---|---|---|
| 0x4000 | 0x34 | 0x12 |
| 0x4001 | 0x12 | 0x34 |
32bit宽的数0x12345678在Little-endian模式以及Big-endian模式)CPU内存中的存放方式(假设从地址0x4000开始存放)为
| 内存地址 | 小端模式存放内容 | 大端模式存放内容 |
|---|---|---|
| 0x4000 | 0x78 | 0x12 |
| 0x4001 | 0x56 | 0x34 |
| 0x4002 | 0x34 | 0x56 |
| 0x4003 | 0x12 | 0x78 |
数组存储
以unsigned int value = 0x12345678为例,分别看看在两种字节序下其存储情况,我们可以用unsigned char buf[4]来表示value:
Big-Endian: 低地址存放高位,如下:
高地址
---------------
buf[3] (0x78) -- 低位
buf[2] (0x56)
buf[1] (0x34)
buf[0] (0x12) -- 高位
---------------
低地址
Little-Endian: 低地址存放低位,如下:
高地址
---------------
buf[3] (0x12) -- 高位
buf[2] (0x34)
buf[1] (0x56)
buf[0] (0x78) -- 低位
--------------
低地址
为什么有大小端
这是因为在计算机系统中,我们是以字节为单位的,每个地址单元都对应着一个字节,一个字节为8bit。但是在C语言中除了8bit的char之外,还有16bit的short型,32bit的long型(要看具体的编译器),另外,对于位数大于8位的处理器,例如16位或者32位的处理器,由于寄存器宽度大于一个字节,那么必然存在着一个如果将多个字节安排的问题。因此就导致了大端存储模式和小端存储模式。例如一个16bit的short型x,在内存中的地址为0x0010,x的值为0x1122,那么0x11为高字节,0x22为低字节。对于大端模式,就将0x11放在低地址中,即0x0010中,0x22放在高地址中,即0x0011中。小端模式,刚好相反。我们常用的X86结构是小端模式,而KEIL C51则为大端模式。很多的ARM,DSP都为小端模式。有些ARM处理器还可以由硬件来选择是大端模式还是小端模式
判断大小端
读取地位地址
定义一个 16 位无符号的整数值,然后判断其低位字节存放的位置
#include <stdio.h>
int main() {
__uint16_t val = 0x1234;
char a = ((char *) &val)[0]; // 低位地址
char b = ((char *) &val)[1]; // 高位地址
printf("a = %x\n", a);
printf("b = %x\n", b);
if (a == 0x34) {
printf("小端模式\n");
} else {
printf("大端模式\n");
}
return 0;
}
通过 &val 取得 val 的内存地址,然后将其转为 char 类型的指针,再以数组的方式取指针地址上存储的值
下标 0 可以取到低位地址上的值,下标 1 可以取到高位地址上的值。如果下标 0 取到的是 0x34,说明是小端模式,因为低位字节存储在低位地址上
C语言内置宏
C 语言已经自带了一些宏用来判断主机的字节序
endian.h文件:
// 小端模式
# define LITTLE_ENDIAN __LITTLE_ENDIAN
// 大端模式
# define BIG_ENDIAN __BIG_ENDIAN
// 当前主机的字节序
# define BYTE_ORDER __BYTE_ORDER
#include <endian.h>
int main()
{
if (BYTE_ORDER == LITTLE_ENDIAN) {
printf("小端模式\n");
} else {
printf("大端模式\n");
}
return 0;
}
大小端转换
这里也不在我想了解范围内,简单记录一下
整型解析
所以整形打印的结果应该是
00 00 00 00 -> 0
00 00 00 01 -> 1
00 00 00 02 -> 2
00 00 00 03 -> 3
这里是用16进制表示
举个🌰
0a 00 00 00 0b 00 00 00 0c 00 00 00 0d 00 00 00
0e 00 00 00 0f 00 00 00 10 00 00 00 11 00 00 00
展开一下就是
00 00 00 0a -> 10
00 00 00 0b -> 11
00 00 00 0c -> 12
00 00 00 0d -> 13
00 00 00 0e -> 14
00 00 00 0f -> 15
00 00 00 10 -> 16
00 00 00 11 -> 17
浮点型
整型对上号了,那浮点型还是对不上啊,突然想到组原学到的浮点类型表示方法
00 00 00 00 00 00 80 3f 00 00 00 40 00 00 40 40
这里的表示应该是
00 00 00 00
3f 80 00 00
40 00 00 00
40 40 00 00
存储方式
计算机对浮点数的表示规范遵循电气和电子工程师协会(IEEE)推出的 IEEE754 标准,浮点数在 C/C++ 中对应 float 和 double 类型,我们有必要知道浮点数在计算机中实际存储的内容
IEEE754 标准中规定 float 单精度浮点数在机器中表示用 1 位表示数字的符号,用 8 位表示指数,用 23 位表示尾数,即小数部分。对于 double 双精度浮点数,用 1 位表示符号,用 11 位表示指数,52 位表示尾数,其中指数域称为阶码。IEEE754 浮点数的格式如下图所示
| 类型 | 长度 | 符号位(Sign) | 指数位(Exponent) | 尾数(Mantissa) |
|---|---|---|---|---|
| float | 32 | 1bit | 8bit | 23bit |
| Double | 64 | 1bit | 11bit | 52bit |
符号位(Sign): 0 表示数值为正数, 1 表示负数
指数位(Exponent): 即为二进制用科学计数法表示的指数部分,其中 float 为 8 位, double 为 11 位,以 float 为例, 8 位的指数为可以表达 0 到 255 之间的 255 个指数值。但是指数可以为正数, 也可以为负数。为了能表示负指数, 实际存储指数值需要加上一个偏移量(Bias)作为保存在指数位中的值。 float 偏移量为 127 (即 8 位指数可以表示 -127 ~ 128 次方)
尾数(Mantissa): 称为浮点数的尾数, 即部分二进制位(小数点后面的二进制位, 它决定了浮点数的表示精度, 即可以给出的有效数的位数), 因为==规定 M 的整数部分恒为1==, 所以这个 1 就不进行存储
移码
移码(又叫增码)是对真值补码的符号位取反,一般用作浮点数的阶码,引入的目的是便于浮点数运算时的对阶操作
对于定点整数,计算机一般采用补码的来存储。正整数的符号位为 0,反码和补码等同于原码。负整数符号位为1,原码、反码和补码的表示都不相同,由原码变成反码和补码有如下规则:
- 原码符号位为1不变,整数的每一位二进制数位求反得反码;
- 反码符号位为1不变,反码数值位最低位加1得补码。
这里规则其实很简单
正整数补码和反码就是本身不需要改变,移码是符号位取反
负整数符号位不变,其余取反得反码,反码最低位加1得补码,符号位取反得移码
举个🌰
| 真值 | 反码 | 补码 | 移码 |
|---|---|---|---|
| +3=00000011 | 00000011 | 00000011 | 10000011 |
| -3=10000011 | 11111100 | 11111101 | 01111101 |
浮点型解析
简单点
3f 80 00 00
0011 1111 1000 0000 0000 0000 0000 0000 // 每个数字写成二进制
40 40 00 00
0100 0000 0100 0000 0000 0000 0000 0000
复杂点
c0 49 0f da
11000000 01001001 00001111 11011010
参考: